Deposited graphene monolayer on certain cubic transition metals provides opportunities for the self assembly of nanostructured materials, which can be used for high density magnetic storage devices. The competition between the two incommensurable lattices gives rise to a Moiré visible by electron microscopy [1].
The purpose of the study consists in investigate the stability of deposited nanoparticles on epitaxial graphene layer on metal by an atomistic approach and emancipate from the DFT size limitation. Thus, the thermodynamic properties of a graphene sheet is studied at zero pressure and finite temperature by Monte Carlo simulations. A variety of carbon potentials were used: the empirical three body potential Stillinger-Weber [2], a serie of seminal potentials based on the N body bond-order potential [3-10], including both short, medium and long-range interactions. Finally a fourth moment tight-binding potential was also used [11].
We first evaluate the ability of potentials to reproduce the in-plane structural properties of graphene in function of the temperature.
The thermal excitation induces large scale graphene ripples [12], resulting in a decrease of the in-plane surface, originate a negative thermal expansion coefficient, α< 0. The simulations showed a wide dispersion and large discrepencies of the lattice parameter and in-plane α. Indeed α(T) show a positive, negative sign or a sign change, depending on the potential [13]. The question concerning the sign of α is currently debated. On the one hand, Fasolino [12] explained the sign change of α by the hanarmonic phonon modes (harmonics) around 900 K, producing stretching (bending) of the graphene monolayer and inducing a sign change (negative sign) of α. However, the elasticity model of de Andres [14] shows that hanarmonic phonon modes are not responsible of the sign change of α. This result in agree with DFT [14-17] and experiences [18,19].
This systematic comparison highlights a strong potential depence that should be used with caution in case of graphene. Note also that a potential specially dedicated to graphene is currently lacking as experimental results beyond the room temperature concerning α.
Metal-substrate interactions were then reparametrized from the Brenner potential [4], showing a qualitative agreement with DFT [17]. The model, was then optimized by the development of an analytical potential describing implicitly the metal substrate [20]. Actually, the model allows to determine the equilibrium structures (Monte Carlo simulations), Figure 1.
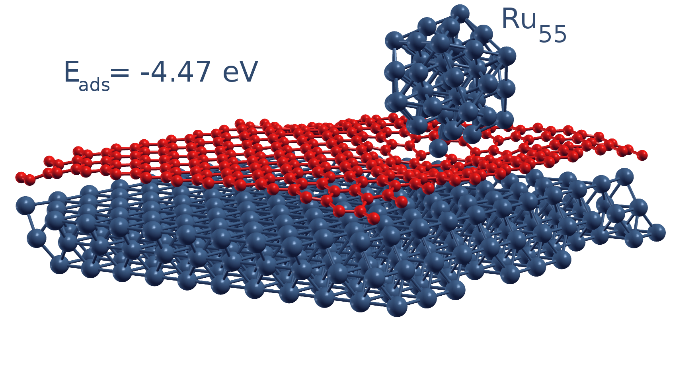Figure 1 :Equilibrium structures composed of a ruthenium nanoparticule deposited on a graphene monolayer on a ruthenium substrate. The interactions between the carbon and ruthenium atoms was reparametrized from the Brenner potential [4].
[1] A.T. N'Diaye et al., Phys. Rev. Lett. 97, 215501 (2006),
[2] F.H. Stillinger, T.A. Weber, Phys. Rev. B 31, 5262 (1985)
[3] J. Tersoff, Phys. Rev. B 37, 6991 (1988)
[4] D.W. Brenner, Phys. Rev. B 42, 9458 (1990)
[5] J. Che et al., Theor. Chem. Acc. 102, 346 (1999)
[6] S.J. Stuart et al., J. Chem. Phys. 112, 6472 (2000)
[7] D.W. Brenner et al., J. Phys.: Cond. Matt. 14, 783 (2002)
[8] L. Lindsay, D.A. Broido, Phys. Rev. B 81, 205441 (2010)
[9] J.H. Los, A. Fasolino, Comp. Phys. Commun. 147, 178 (2002)
[10] J.H. Los, A. Fasolino, Phys. Rev. B 68, 024107 (2003)
[11] H. Amara et al., Phys. Rev. B 79, 014109 (2009)
[12] A. Fasolino, Nature Mater. 6, 858 (2007)
[13] Y. Magnin et al., J. Phys.: Cond. Matt. 26, 185401 (2014)
[14] P.L. de Andres et al., Phys. Rev. B 86, 144103 (2012)
[15] N. Mounet, N. Marzari, Phys. Rev. B 71, 205214 (2005)
[16] F.L. Huang, Z. Zeng, J. Appl. Phys. 113, 083524 (2013)
[17] M. Pozzo et al., Phys. Rev. Lett. 106, 135501 (2011)
[18] D. Yoon et al., Nano. Lett. 11, 3227 (2011)
[19] A.K. Singh, R.G Hennig, Phys. Rev. B 87, 094112 (2010)
[20] G.D. Förster et al., Model. Simul. Mater. Sci. Eng. 22, 035015 (2014)